卷积神经网络可以如何优化？

卷积神经网络除了自身的参数调整和卷积层的选择，还有哪些方面可以做优化呢/

还可以引入软阈值化。

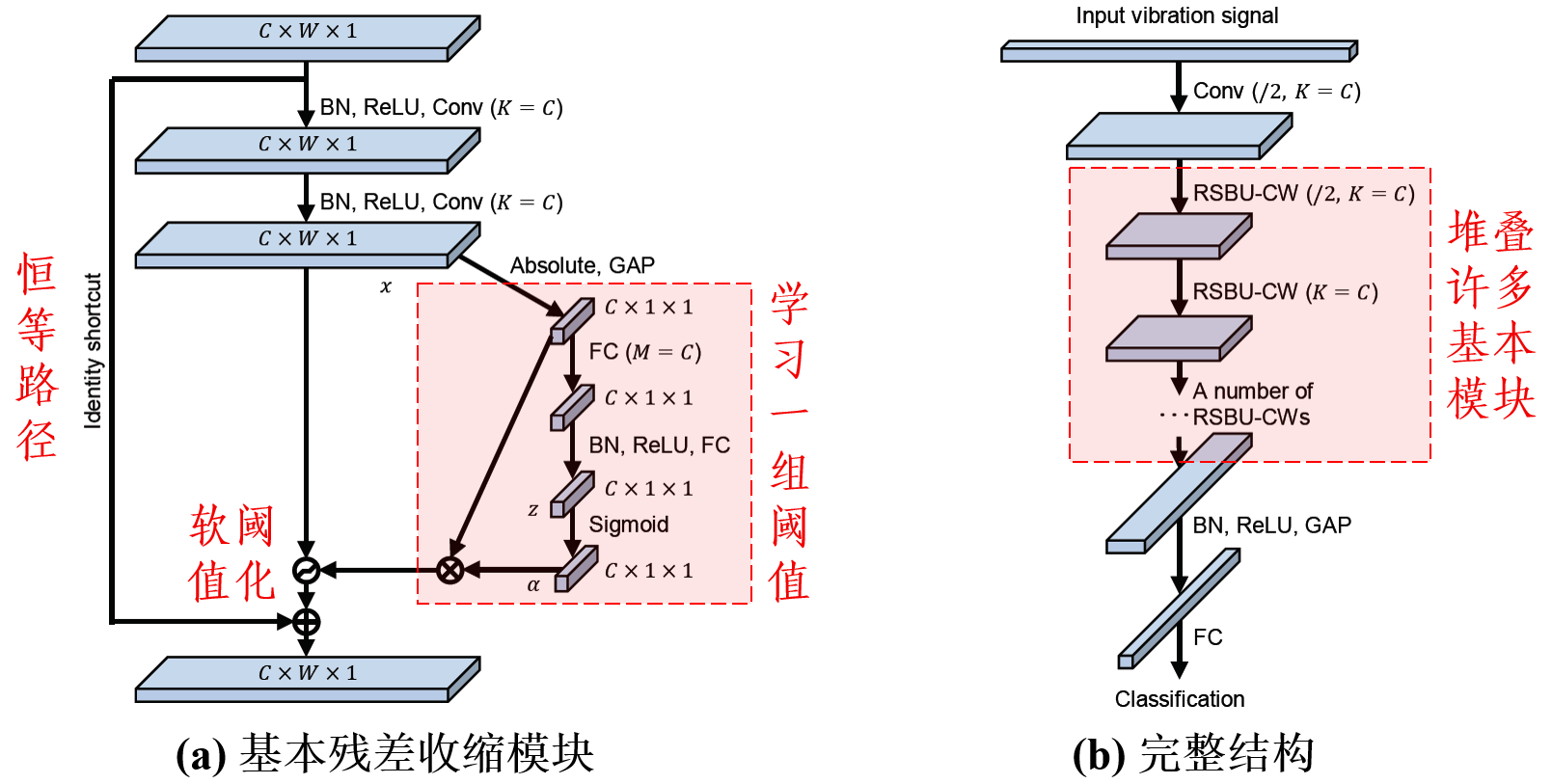
软阈值化是降噪时的常用函数。在卷积神经网络中引入软阈值化，可以增强其在含噪数据上的效果。

其中，最典型的就是深度残差收缩网络^[1][2]：

前几天写了一个卷积神经网络（CNN）中，卷积和加法融合的文章。有同学问，希望写一个带代码版本的，方便更好的理解。

我的第一反应是，代码版本的咋写，有那么多细节。后来一想，其实那位同学想知道的并不是那些细节，而是一个大致的流程。

那我就简单写一个伪代码版的吧，把大致的代码思路写一下。

至于具体卷积算法怎么实现的，建议chatGPT一下，或者看下开源深度学习仓库就行。

如果没看之前的文章，可以看上一看：简单有效的卷积和加法的算子融合

还是以 resnet50 中的图为例，做一个卷积和加法的融合。

正常情况下，上述网络片段在执行的时候大概是这样的：

BatchNorm -> Relu -> Conv -| Add的左分支
                           |                -> Add
                  -> Conv -| Add的右分支

写出伪代码，实际上就是一种顺序调用逻辑，比如

bn_out=Batch_normal();
relu_out=Relu(bn_out);
conv_out_left=Conv2d(relu_out)
conv_out_right=Conv2d(...)
add_out=Add(conv_out_left, conv_out_right)

而一旦融合完之后，上图红框中的Conv 和 Add 就变成了一个算子，这里暂且称这个融合之后的算子为 ConvAdd 算子。

于是，上述的图，就变成了如下的图：

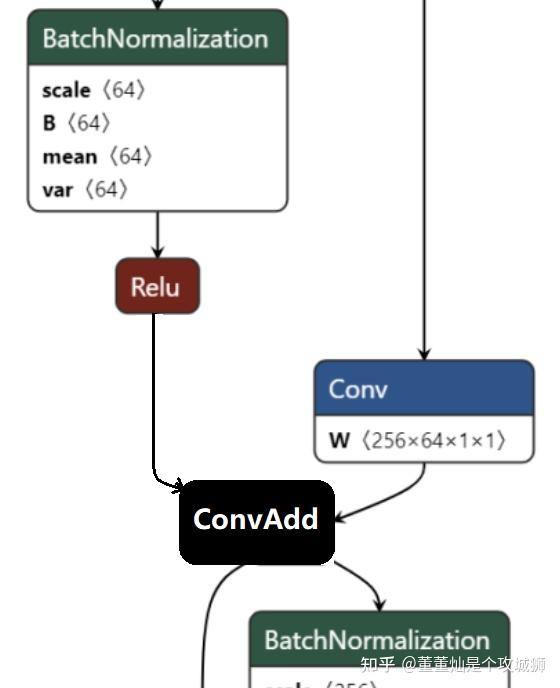
此时，整个网络片段的调用逻辑变成了：

bn_out=Batch_normal();
relu_out=Relu(bn_out);
conv_out_right=Conv2d(...)
add_out=ConvAdd(relu_out, conv_out_right)

再把 ConvAdd 当做一个算子之后，便可以进行很多融合、拆图、流水并行操作。

假设现在这个网络运行在一个Asic芯片上，芯片上卷积计算模块和加法计算模块是互相独立的，没有任何依赖。

这里假设卷积输入的 Feature Map 的大小是[n, hi, wi, ci]，卷积核是[co, kh, kw, ci]。

其余参数简化一下，将卷积 pad 简化为0，stride 简化为1，dilation简化为1。

卷积的输出为[n, ho, wo, co]。

那么卷积后面的加法，执行的两个tensor相加，也就变成了[n, ho, wo, co]+[n, ho, wo, co]=[n, ho, wo, co]。

那么，我们将卷积的输入（假设是下面的一张图），在H方向切成两份。

那么计算完一整张图，需要调用两次卷积运算，第一次计算上半部分，第二次计算下半部分。

两次计算中，大部分像素之间是没有关系的，仅仅在两部分交界的地方会有可能存在依赖。（存在依赖的条件为 kernel 大于1，或者 stride 大于1，这些情况先不考虑，暂时认为两部分像素没有关系）。

那么第一次卷积计算，计算的输入是 [n, hi/2, wi, ci]，计算输出结果是[n, ho/2, wo, co]。此时计算的是前半部分的 hi。用加黑表示。

那么第二次卷积计算，计算的输入是 [n, hi/2, wi, ci]，计算输出结果是 [n, ho/2, wo, co]。此时计算的是后半部分的 hi。用斜体表示。

同理，加法也会被分成两次计算，分别对应计算卷积的两次输出：

第一次加法，计算的是第一次卷积的输出，即[n, ho/2, wo, co]。

第二次加法，计算的是第二次卷积的输出，即 [n, ho/2, wo, co]。

那么，在两次计算的情况下，ConvAdd 这一个算子中，内部的实现逻辑大致应该是：

conv_out_part1=Conv2d(part1)
conv_out_part2=Conv2d(part2)
add_out_part1=Add(conv_out_part1)
add_out_part2=Add(conv_out_part2)

但是这样显然是不行的，因为这样写还是串行执行：执行完第一次卷积执行第二次卷积，执行完第二次卷积执行第一次加法...那怎么让 Conv 和 Add 并行起来呢？

通过观察可以发现，第一次的Add并不依赖第二次的Conv，并且我们已经假设了Asic芯片上Conv运算模块和Add模块完全独立。

那么让第二次Conv和第一次Add并行起来的方法就是：第一次Conv计算完之后，直接计算第一次Add，然后同时并行第二次Conv，这个时候，代码的实现大致是这样：

conv1=Conv2d(part1)
-----------------------
add1=Add(conv1)      
conv2=Conv2d(part2) 
-----------------------
add2=Add(conv2)

这个时候，Add 和 conv 在中间的一个流水级中并行起来了。

所谓的一个流水级，指的是上面代码段中两个“ ------ ” 之间的代码，称之为在一个流水级中。

那如果将图片拆成更多份，那可以并行的流水级就会更多。

比如拆成4份，那可以有3个流水级中的Conv和Add并行起来。

conv1=Conv2d(part1)
-----------------------
add1=Add(conv1)      
conv2=Conv2d(part2) 
-----------------------
add2=Add(conv2)
conv3=Conv2d(part3) 
-----------------------
add3=Add(conv3)      
conv4=Conv2d(part4) 
-----------------------
add4=Add(conv4)      
-----------------------

需要说明一点的是，上面伪代码中，每一个 “-----” 其实都代表了一个同步点。在实际部署到硬件上运行时，需要在这些同步点上设置同步操作，用来使上一个流水级中的所有计算操作全部完成即可。

常用的同步操作有一些同步指令或者barrier指令。假设我们使用barrier指令来进行同步，那么上述完整的伪代码便是：

conv1=Conv2d(part1)
barrier()

add1=Add(conv1)      
conv2=Conv2d(part2) 
barrier()

add2=Add(conv2)
conv3=Conv2d(part3) 
barrier()

add3=Add(conv3)      
conv4=Conv2d(part4) 
barrier()

add4=Add(conv4)      
barrier()

当然上述代码看起来太长了，可以写成循环的形式，还是以将H方向拆分 4 份为例：

conv1=Conv2d(part1);
barrier();

for i in range(1, 4):
    add_i=Add(convi)
    Conv_i+1=Conv2d(part_i+1)
    barrier()

add4=Add(conv4)      
barrier()

伪代码的逻辑还是很简单的，关键是需要理解Conv和Add并行流水的思想。

这种方法可以用到的融合场景很多，并不仅仅局限于Conv和Add这两个算子，也不局限于某一个神经网络。

只要是在硬件上计算单元可以并行执行，并且在神经网络结构图上前后有依赖的层，几乎都可以这么进行融合来提升整体性能。

码字不易，欢迎关注 @董董灿是个攻城狮 及同名公众号 董董灿是个攻城狮，一起学习深度学习。

本篇回答主要从 CV 领域作答。在 CV 领域中，卷积计算是扩充像素的感受野的有效方法，模型大多数的计算量都是卷积操作贡献的。因此在 CV 模型的推理性能优化中，最重要的一项工作是对卷积的优化。MegEngine 在长期的工业界实践和反馈的基础上总结得出卷积优化的基本方法有：

• 直接卷积计算优化

该方法的计算过程为逐通道进行卷积滑窗计算并累加，该优化方法对卷积的参数敏感，为了达到最优的性能，会根据各个卷积参数分别进行 kernel 优化，通用性弱，但是在 Depthwise 的卷积中却是最高效的方法。

• FFT 卷积计算优化

根据卷积的性质，利用傅立叶变换可以将卷积转换为频域上的乘法，在频域上的计算对应乘法，再使用傅立叶变换逆变换，就可以得到卷积对应的计算结果。该方法使用高性能的傅立叶变换算法，如 FFT，可以实现卷积计算的优化，算法性能完全取决于傅立叶变换的性能以及相应卷积参数。

• Im2col+matmul 卷积计算优化

由于卷积计算中有大量的乘加运算，和矩阵乘具有很多相似的特点，因此该方法使用 Im2col 的操作将卷积运算转化为矩阵运算，最后调用高性能的 Matmul 进行计算。该方法适应性强，支持各种卷积参数的优化，在通道数稍大的卷积中性能基本与 Matmul 持平，并且可以与其他优化方法形成互补。

更多详情见：

• Winograd 卷积计算优化

Winograd 方法是按照 Winograd 算法的原理将卷积运行进行转变，达到减少卷积运算中乘法的计算总量。其主要是通过将卷积中的乘法使用加法来替换，并把一部分替换出来的加法放到 weight 的提前处理中，从而达到加速卷积计算的目的。Winograd 算法的优化局限为在一些特定的常用卷积参数才支持。

由于 direct 卷积可以直接由公式得来，而 FFT 卷积对于当前业界用到的各种参数的卷积，其性能优势远没有其他优化方法明显，对于这两者本文不做详细展开。这里主要讲述 Im2col 和 Winograd 算法的实现以及优化方法。

更多详情见：

查看文档、 MegEngine 官网和 GitHub 项目，或加入 MegEngine 用户交流 QQ 群：1029741705

随着深度学习的发展，当面对复杂问题的时候，在深度神经网络提取特征的过程中完全抛弃知识是非常不明智的策略。虽然有很多研究者在深度网络处理数据之前， 利用具有某种知识的模型驱动方法对数据进行预处理， 但是这种方法没有进行实质性地改造深度网络， 且这种两阶段方法从端到端学习策略来看很难达到最优。另一方面， 具有某种知识的模型驱动方法如Schmid滤波器能够保持旋转不变性， 这类知识很符合深度网络中浅层网络结构所需要的特征。因此， 很多研究者利用具有某种知识的模型驱动方法来改进深度网络的网络结构， 用这种方法在深度网络中融入知识能够提高模型的性能。

这方面的研究主要分为三个大方向： 通过知识对输入进行编码并添加到神经网络的输入端构建第一层网络、利用知识改变神经网络的部分结构、利用知识改变神经网络的整体结构。

第一种方式是通过编码知识作为神经网络的辅助输入构建第一层网络的方式实现的，比如利用文本信息作为辅助输入的算法。

第二种方式是通过改变神经网络的部分结构（如：卷积神经网络中的卷积核）实现的： 为保持深度网络往边缘以及纹理信息的方向进行端到端学习，利用Gabor 滤波器改进深度网络的网络结构， 如使用固定参数Gabor滤波器作为第一卷积层的卷积核方法，使用Gabor 滤波器初始化卷积核的方法； 使用Gabor滤波器和普通卷积核相乘的方法。这一类方法的优点在于适当调整网络的部分结构， 从而将知识嵌入到整个深度网络学习的过程中， 缺点在于大部分方法对于初始化或参数的选择要求都很高， 且这些参数难以更新。

第三种方式是通过对整个神经网络的结构作出调整实现的，比如为了保全局信息和边缘信息将多尺度全卷积残差网络和病变指数计算单元结合组成的框架结合以同时处理病变分割和病变分类，这类利用具有某种知识的模型驱动方法改进深度网络框架的方法， 虽然有效地将知识和数据融合改进深度网络， 但是仍然需要更多的数据去训练深层网络。

此外

很多研究者发现这种纯端到端学习策略并不能完全替代具有某种知识的模型驱动算法， 很难处理一些复杂问题如图像去噪， 为了更好地将知识和数据融合改进深度学习方法， deep unrolling技术被提出，deep unrolling技术是一种具有某种知识的模型驱动方法和深度学习方法的迭代交融学习方法， 以弥补将知识和数据融合进行一次简单串行的缺陷。这类技术指的是通过知识建立原始模型并给出基础迭代格式， 然后在此基础上通过引入可学习模型（ 深度网络） ， 进而从给定的训练数据中学习该问题的潜在规律和数据分类， 最后通过unrolling实现知识和数据的有效融合。

unrolling是指将求解一个给定连续模型的迭代优化看成一个动态系统， 进而通过若千个可学习模块（深度网络） 来离散化这一系统，得到数据驱动的演化过程的方法。主要包括的三个核心步骤， 即设计迭代格式、嵌入可学习模块和理论分析； 现有的很多工作都是集中在前面两个步骤中，而由于使用可学习模块对迭代格式进行非精确的展开和计算， 原有的数值算法的理论性质如收敛性不在保持。现有的工作缺乏对这方面的一些研究， 另外unrolling技术仍然是将知识的模型驱动方法和深度学习方法进行简单的串行。

Lee et al., “Resource-Efficient Convolutional Networks: A Survey on Model-, Arithmetic-, and Implementation-Level Techniques,” ACM Comput. Surv., p. 3587095, Mar. 2023, doi: 10.1145/3587095.

CNN部署的三层优化：

• 模型级：对模型架构的改进
• 算术级：使用低精度算法减少内存占用和数据传输
• 实现级：功能相同的情况下采用更有效的实现算法

• 二值量化

使用一位bit来表示权重中的一个元素。二值量化消除了MAC计算中的乘法，若激活也被量化，则CNN中所有MAC操作可以通过XNOR和计数器实现。

• 三元量化

相比二值量化提高了精度，所有权值可以量化为三个值，只需要两个bit来表示量化权重。

• 混合量化

将激活和权重量化为任意低精度格式。例如将权值量化到1位，激活到2位提高了精度。

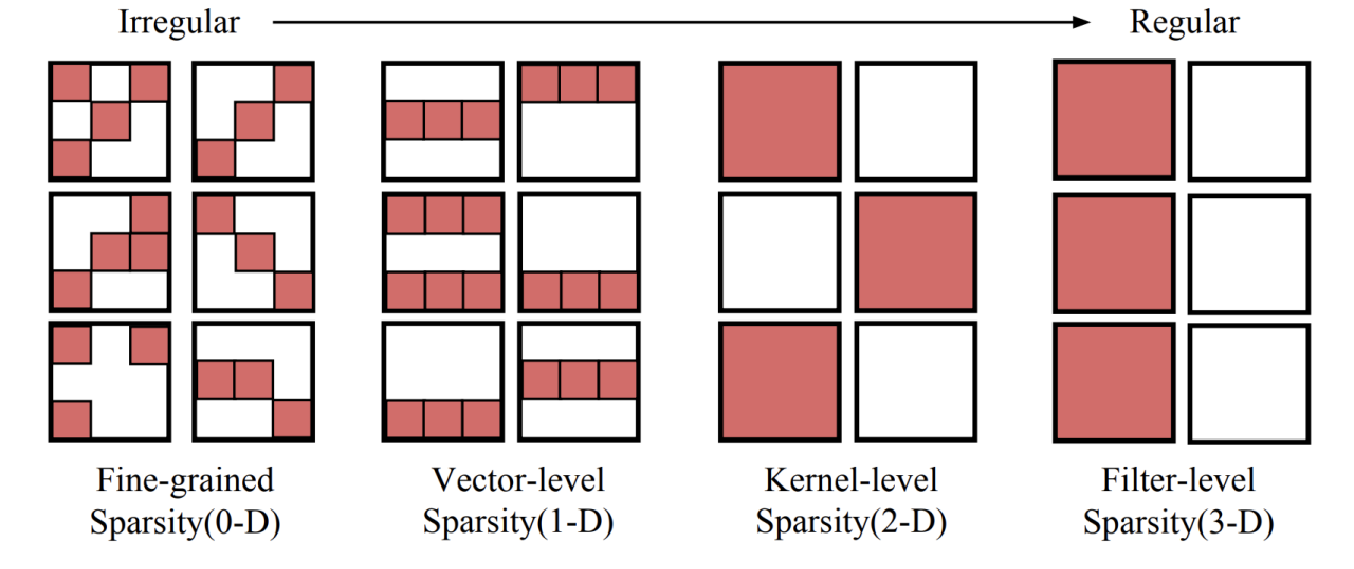
剪枝有多种粒度，越规则化就越粗粒度，可能导致较低的精度和剪枝率，但易加速。

• 压缩通道

SqueezeNet每个网络块利用小于输入通道数量的1×1 filter来减少挤压阶段的网络宽度，然后在扩展阶段利用多个1×1和3×3 kernel。通过挤压宽度，计算复杂度明显降低，同时补偿了扩展阶段的精度。SqueezeNext在扩展阶段利用了可分离的卷积；一个k×k的filter被分为一个k×1和一个1×k的filter。与SqueezeNet相比，这种可分离的卷积进一步减少了参数的数量。

• 深度可分离卷积

深度可分离卷积由Depthwise Convolution和Pointwise Convolution两部分构成。Depthwise Convolution的计算非常简单，它对输入feature map的每个通道分别使用一个卷积核，然后将所有卷积核的输出再进行拼接得到它的最终输出，Pointwise Convolution实际为1×1卷积。最大优点是计算效率非常高。典型实例如 Xception、MobileNet。

• 线性瓶颈层

瓶颈结构是指将高维空间映射到低维空间，缩减通道数。线性瓶颈结构，就是末层卷积使用线性激活的瓶颈结构（将 ReLU 函数替换为线性函数）。该方法在MobileNet V2中提出，为了减缓在MobileNet V1中出现的Relu激活函数导致的信息丢失现象。

• 组卷积

在组卷积方法中，输入通道分为几组，每组的通道分别与其他组进行卷积。例如，带有三组的输入通道需要三个独立的卷积。由于组卷积不与其他组中的通道进行交互，所以不同的组之间的交互将在单独的卷积之后进行。与使用常规卷积的cnn相比，组卷积方法减少了MAC操作的数量

• Octave 卷积

通过在卷积中分离高频和低频信息，压缩模型参数个数，节省特征图的内存占用。

• 降采样

例如更大的卷积步长

• 低秩近似

利用奇异值分解压缩卷积层的参数

主要思想是：学生模型模仿教师模型，并获得近似甚至更优越的性能表现。关键问题是如何将大教师模型转移到小的学生模型上。知识蒸馏系统基本由三个关键部分组成：知识、蒸馏算法、教师-学生结构

知识蒸馏（一）概述 - 知乎 (zhihu.com)

在精度、资源约束、推理性能的要求下，自动搜索出一个可用的小型网络。

• 半精度、单精度和双精度
  
• BFloat16（Brain Float-Point using 16 Bits）
  

谷歌提出的浮点数值类型，支持比FP16更广泛的动态数据类型。目前已用于NVIDIA A100、Google TPU

• DLFloat
  
• TF32（TensorFloat32）
  

Nvidia提出，在其显卡上有专门硬件支持

• 低精度算术
  
• 权重编码
  

利用大多数权重的指数值位于一个狭窄的范围内这一事实，使用Hufman编码方案对权重的频繁指数值进行编码。位于内存和FP算术单元之间的查找表被用来将编码后的指数值转换为FP指数值。

根据前向传播、激活梯度更新、权值更新等不同的训练过程来调整算术精度，可以加速CNN的训练。

• 混合精度训练

1）IFP16+IFP32；2）BFloat16+IFP32；3）FP8+DLFloat；4）DLFloat Only；5）INT8 Only；6）逐层自适应量化

• 使用靠近PE的SRAM本地内存、
  
• 利用空间体系结构
  

采用脉动阵列等设计

• 电路优化

• 转换为矩阵乘法，利用高度优化的矩阵计算库来加速
• im2col
• FFT
• Winograd

• 运行时跳过操作

当使用Relu后许多值变为0，可以在运行时动态跳过

• 编码稀疏权值、激活值、特征图

稀疏矩阵编码

• 早期退出

用于分布式计算系统

• 运行时通道宽度自适应

在运行时修剪了不重要的filter

• 运行时模型切换

DNN的推理延迟由于新分配的工作负载而增加时，运行时决策者在运行期间降级当前DNN以满足延迟约束。当内存资源充足时，这种模型切换方法在运行时是合适的，因为多个dnn应该预装在DRAM中。