Journal of Aerospace Science and Technology
Vol.
07
No.
01
(
2019
), Article ID:
28784
,
10
pages
10.12677/JAST.2019.71001
Research on Topology Optimization Method for Typical Wings
Hongjuan Zhao, Weihang Lin, Chuang Wei, Jiayi Du
College of Aerospace Engineering, Shenyang Aerospace University, Shenyang Liaoning
Received: Jan. 12th, 2019; accepted: Jan. 27th, 2019; published: Feb. 3rd, 2019

ABSTRACT
In order to solve the structural design problem of wing, topological optimization technology is introduced in the optimization design of wing structure. By means of variable density method, the mathematical model of “taking the minimum flexibility of the wing as the objective function and the volume reduction percentage as the constraint condition” was established. ANSYS software was used to conduct static finite element analysis of the wing, and the topology optimization design of the wing structure under different working conditions was carried out. The basic model establishment, optimization and non-optimization region determination, optimization criterion selection and optimization result analysis and application are discussed in topology optimization design. The results show that the topology optimization method is correct and effective, and has a certain application prospect in the optimization design of wing structure.
Keywords:The Wing, Finite Element Analysis, Topology Optimization, ANSYS
典型机翼的拓扑优化方法研究
赵红娟,林伟航,魏闯,杜家毅
沈阳航空航天大学,辽宁 沈阳
收稿日期:2019年1月12日;录用日期:2019年1月27日;发布日期:2019年2月3日

摘 要
针对机翼的结构设计问题,引入拓扑优化技术在机翼结构最优化设计中,采用变密度方法,建立了“以机翼最小柔度为目标函数,体积减少百分比为约束条件”的数学模型,利用ANSYS软件对某飞机机翼进行静态有限元分析,对不同工况下的机翼结构进行拓扑优化设计。探讨了拓扑优化设计过程中,基本模型建立、优化与非优化区域确定、优化准则选取及优化结果分析与应用等问题。研究结果表明,该结构拓扑优化方法的正确性和有效性,在机翼结构优化设计中具有一定的应用前景。
关键词 :机翼,有限元分析,拓扑优化,ANSYS

Copyright © 2019 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
结构优化主要是为了满足设计中使材料用量最少、成本达到最低、工艺步骤最简单的最优标准。从工程设计角度,结构优化可分为尺寸优化、形状优化以及拓扑优化三个层次。尺寸优化和形状优化已经得到充分的发展,在航空、航天、桥梁、汽车等一些领域得到了广泛的应用 [1] ,但它们在结构设计中存在一定的局限性,所以拓扑优化设计方法应运而生。拓扑优化设计是结构的尺寸优化设计和形状优化设计之后,一种最具有挑战性的研究课题,同时也是具有简单、高效、经济的设计方法,成为近年来结构优化设计研究的热点。
飞机结构重量是影响飞机各项性能指标的重要因素。机翼作为飞机设计中重要的组成部分,其结构轻量化是提高各项性能指标的基础。机翼是飞机最主要的提供升力的部件,如何设计出重量轻、强度高、刚度大的结构布局是设计师面临的主要任务 [2] 。在传统的结构设计中,设计者需要根据自己的经验及以前的飞机型号作参考。定义机翼零件尺寸大小以及相应位置,然后通过试验和数据分析校核检验设计结果。对于结构进行多次修改、校核检验分析,直到满足设计要求。这种方法过程繁杂、耗时耗力,过于依赖设计者的经验和判断,缺乏统一设计的准则和依据 [3] 。随着设计人员的不断探索,发现飞机结构拓扑优化设计方法恰好可以解决传统方法中存在的问题。拓扑优化设计主要是借助计算机软件建立相应的几何模型,对设计要求进行分析论证,通过有限元理论和基本力学原理对结构模型进行分析,实现机翼各部分结构的布局设计,为设计人员提供一套完整的、准确的且具有实际应用价值的理论依据和设计方案 [4] 。拓扑优化方法能够有效降低飞机的重量、通过对材料进行合理布局,提高其使用效率,进而使飞行器的整体性能达到最优。
就结构设计而言,我们可以理解为依据设计对象的载荷情况,有目的性地设计其材料的分布,确定合理的承载力结构。在设计过程中,根据载荷在结构内的分布方式,进而得到设计对象的最优拓扑结构。根据受载情况,设计出满足要求的结构形式,材料得以充分有效利用,因此这种类似于传力路径的研究十分重要 [5] 。而拓扑优化方法不仅可以具体分析结构的传力路径,还可以实现对其优化设计,为寻求最优、最合理的结构形式提供理论依据 [6] 。
在以往,国内通常采用替换钢和铝合金材料为复合材料来减轻重量,国外一般采用结构优化设计的新技术降低重量。本文结合拓扑优化方法,根据机翼某种状态下受气动载荷情况进行分析,在满足各项性能指标的条件下,实现机翼结构合理布局,达到质量尽可能轻,且最优的传力路径的机翼拓扑结构。
2. 拓扑优化设计模型
2.1. 优化方法的选择
拓扑优化的研究领域主要分为两种:即离散结构拓扑优化和连续体拓扑优化,两种领域都需要在有限元方法基础上展开和应用的。1904年,Michel提出了Michel桁架理论,满足此理论的结构通常被称为最小重量桁架。到1964年Dorn、Gomory、Greenberg等人提出基结构法,在数值分析领域内引入拓扑优化技术,从此打破了Michel桁架理论中存在的局限性,使拓扑优化理论活跃起来。由于优化模型离散方法困难和大规模的计算量,使拓扑优化方法发展有些缓慢。1988年Kikuchi和Bendsoe等人提出均匀化方法 [7] ,为拓扑优化方法打下了坚实的基础,引起了连续体拓扑优化的快速发展,随着学者们的不对深入研究,相继提出渐进结构优化法 [8] 、水平集方法 [9] 以及变密度法 [10] 等,从此,拓扑优化方法在学术界得到取得了稳定的地位,并广泛的被应用。
2.2. 变密度法数学模型
变密度法(Variable Density Method)是1993年Mlejnek在受均匀化方法的启发下提出的,它开启了结构拓扑优化又一个高效的数学方法,Mlejnek在均匀化方法的经验和成果基础上,假定设计结构的材料弹性模量与其密度的非线性关系,使它在宏观层面上显示了优化的拓扑结构及微观层面上的材料密度分布方式。变密度法是最为普遍应用的方法,其基本思想是:引入一种假想的相对密度(即伪密度)在0~1之间的可变密度材料,通过伪密度的分布确定拓扑结构,所以需要假定伪密度与弹性模量之间的某种特定关系,然后定义每个单元伪密度作为设计变量,以材料的分布方式来实现拓扑优化结构。变密度法将拓扑优化在0和1之间的取舍离散性问题转换为在0~1之间取值连续的优化问题。其中,0表示结构中无材料填充,1表示结构为实体单元,0~1之间表示结构为过渡材料(灰度单元)。为了消除灰度单元使结构满足最优拓扑结构,引入惩罚因子对伪密度在0~1之间的结构单元进行惩罚,使拓扑优化模型更好的逼近0或者1的离散优化模型。以体积为约束条件,结构最小柔度为目标函数,变密度法的拓扑优化模型可表示为:
(1)
式中,x为单元伪密度,C为结构柔度,F为结构载荷,K为总刚度矩阵,U为结构总体位移,k0和ue分别为单元刚度矩阵和单元位移矩阵,f为体积分数,V(x)为保留的体积,V0为初始的材料体积。p为惩罚因子。设计变量下限值通常取xmin=0.001,可以有效地避免刚度矩阵产生奇异。
3. 机翼受力分析
3.1. 受力分析的目的
主要是运用软件,采取有限元分析的方法,通过给机翼加载其在巡航状态下所受的各种力,来分析机翼各部件所受的力以及它们在这些力作用下的变形,根据结果来修改机翼的结构设计,以达到即能保证机翼在飞行时的气动外形,又能合理设计出各个部件的最佳设计尺寸,最终解决机翼满足强度、刚度要求情况下得到最少重量的问题。
采用有限元分析方法,通常是最有效的机翼受力分析方式。为了使有限元分析的结果比较准确的接近现实,就必须较好的完成以下两个工作。
1) 较为准确的绘制机翼的三维几何模型图,本文采用CATIA进行绘图。
2) 在有限元分析时,要想比较接近现实结果,就必须比较准确的加载机翼在巡航状态下所受的各种载荷,对于机翼我们可以把其看作悬臂梁来处理,同时分析机翼的受力情况。
3.2. 机翼结构的传力路径分析
机翼结构的优化设计其主要任务是对传力路径分析,具体的分析方法为:
1) 对结构进行合理简化,略去次要元件和次要部分,从而使在传力分析中,减少结构存在的静不定问题。
2) 对结构中各元件之间的连接关系了解清楚,并合理简化铰链、固接等集中连接或分散连接的典型连接形式。
3) 根据结构初始外载荷,以及各结构的受力情况,合理的简化成典型的受力构件,由静力平衡条件,确定各构件的受力情况。
4. 机翼载荷特点
4.1. 机翼受载荷情况
机翼是对称结构,如图1所示,分析机翼在某种巡航状态下的载荷情况。
1) 空气动力载荷
空气动力载荷q为分布载荷,在机翼的表面上,以吸力或者压力形式存在,表现为机翼的升力或阻力。其中升力是机翼最主要的外载荷,不同的设计情况下,机翼的气动载荷数值和分布情况不同,因此其合力的大小、方向、作用点相应地也不同,并将影响机翼的受力情况。
2) 机翼结构的质量力
机翼结构的质量力Q是分布载荷,其大小和分布主要由机翼的结构质量决定,质量力的大小相比于气动载荷要小很多。工程计算中,它的分布规律近似的认为与弦长成正比。
3) 其他集中载荷
机翼上存在其他载荷,如起落架、发动机等连接部件传来的载荷,油箱、炸弹等布置在机翼内、外的各种载荷,通常它们是以有限的连接点连接到机翼主体结构,主要以集中载荷的形传递给机翼,有些力的数值可能比较大。

Figure 1. Distributed and concentrated loads on wings
图1. 机翼受到的分布载荷和集中载荷
4.2. 机翼结构有限元分析
机翼作为飞机提供升力的主要部件,其结构必须满足足够的强度、刚度、耐久性和损伤容限等多方面要求,同时还应有合理梯度载荷模型实现气动载荷分布。对机翼结构优化设计特点分析,控制边界条件,施加气动载荷是飞机整体设计的基础和重点,决定着整体分析结果的正确性和有效性。利用有限元法对机翼结构进行分析,了解机翼载荷情况,简化机翼模型,进行网格划分建立有限元模型。

Figure 2. Finite element model
图2. 有限元模型
有限元模型最基础的是几何模型的建立。建立几何模型的方法大致分为两类:一是基于ANSYS的建模功能建立几何模型;二是从其他建模软件建立几何模型,通过转换为igs或者stp格式并导入到ANSYS中进行分析。本文主要使用PROFILI软件获取机翼翼型,通过CATIA设计尺寸,建立三维空间几何模型,通过接口程序导入到ANSYS中,进行网格划分和计算求解。有限元模型中总共9600个单元,24,000个节点。如图2所示。
5. 机翼拓扑优化
机翼结构拓扑优化,首先略去次要元件和次要部分,对原结构进行合理简化,着重研究参与总体传力的主要部分和主要元构件,寻找载荷传递的的最佳分配方案。主要表现为最小柔度(即最大刚度)拓扑优化设计。与传统优化设计相比,拓扑优化的目标函数、设计变量和状态变量都是预先设计好的,只需要定义材料模型、属性、载荷以及需要减少的体积百分比。拓扑优化的目标函数是满足以体积为约束条件下,利用有限元分析中设计变量的单元伪密度,实现结构柔度最小,相当于提高结构的刚度要求。
5.1. 定义拓扑优化问题
定义拓扑优化问题同定义其他线性,弹性结构问题做法一样,设定材料弹性模量为1.1e09Pa,泊松比为0.3,然后根据分析对象的基本结构建立机翼优化模型。
5.2. 单元类型的选择
根据ANSYS对拓扑优化单元的设定,支持拓扑优化功能的单元相对较少,对于三维实体单元通常选SOLID92或SOLID95。其中,SOLID95是20节点的六面体高阶单元,是在8节点六面体单元的12条边中间增加一个节点,其更适合用于高精度设计要求,且曲线边界的几何模型中。本文选取20节点SOLID95单元进行拓扑优化。
5.3. 定义和控制载荷工况
施加载荷时需要搞清楚机翼受载荷情况,根据上述分析,在机翼翼根处施加位移载荷,上表面施加分布载荷,如图3所示。

Figure 3. Constraint and Load Display
图3. 约束和载荷显示图
5.4. 定义和控制优化过程
拓扑优化过程主要为:定义结构优化区域、确定目标函数和约束条件、选取合理的优化算法、判断收敛性、查看优化结果,主要流程如图4所示。
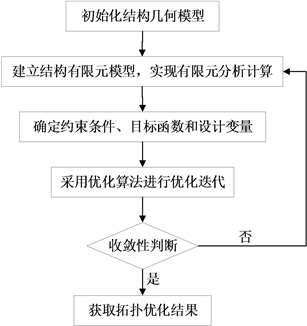
Figure 4. Topology optimization process
图4. 拓扑优化流程
1) 优化算法的选取
拓扑优化求解过程需要寻求收敛速度快且简单高效的算法,快速的寻找到全局最优解。本文选取优化准则法 [11] 进行求解,主要的求解步骤是:定义初始化设计变量,判定收敛性后进行有限元分析,得到相应的位移函数,定义目标函数并进行灵敏度分析,应用过滤技术更新设计变量,直到目标函数收敛。对于最小柔度问题,更新设计变量的OC法优化方案可表示为:
(2)
式中:m为移动限制量,它是伪密度改变区间值,为了使优化迭代过程中尽可能的保留有效的单元数,m在0.1~0.3之间取值,通常取m=0.2。Be是根据结构最优化条件中推导出来的,其数学模型可表示为:
(3)
式中:λ是拉格朗日乘子,从而目标函数的灵敏度可表示为:
(4)
利用式(2)对连续体结构拓扑优化过程中的设计变量进行更新,进而在约束条件的限制下使目标函数逐渐减小,直到达到设计要求。
2) 给定优化条件
设定流速0.5马赫,迎角5度,定义材料弹性模量为1.1e09Pa,泊松比为0.3,体积减少百分比为70%,收敛容差为0.0001。以体积为拓扑优化约束条件,最小柔度(即最大刚度)为拓扑优化目标函数,采用优化准则法(OC)进行结构拓扑优化。进行50次优化迭代使体积减少70%。其拓扑优化命令流如表1所示。
Table 1. System resulting data of standard experiment
表1. ANSYS优化迭代命令流
5.5. 查看拓扑优化结果
通过拓扑优化处理后,根据密度分布云图可知(如图5),红色表示要保留的材料,蓝色表示可以去掉的材料,中间颜色为过渡材料。
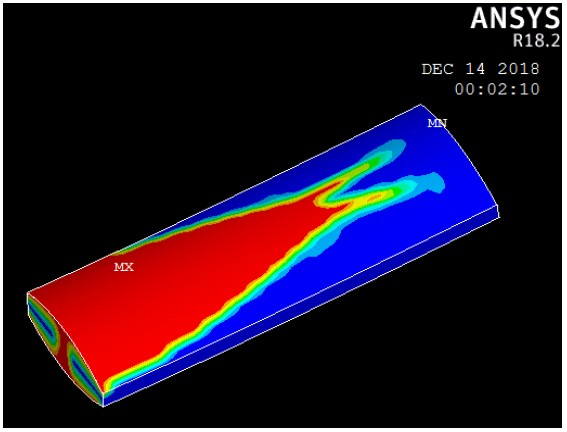
Figure 5. Topology optimization density
图5. 拓扑优化密度云图
通过后处理器根据表2命令流查看密度等值图,其拓扑优化后内部结构如图6所示,可以看出,根据材料分布得到了机翼内翼肋和翼梁的雏形,其结构形式为多梁结构(或多墙结构),根据图7可以得出,在满足技术要求的前提下,目标函数收敛。
Table 2. System resulting data of standard experiment
表2. 后处理命令流

Figure 6. Internal structure display
图6. 内部显示图
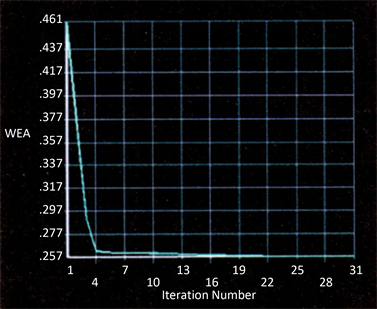
Figure 7. Object Function Curve
图7. 目标函数曲线图
为了拓扑结果更好的利用在实际工程中,将结构进行后处理,根据内部结构图建立翼梁翼肋数目,得到如图8所示的多梁加肋的机翼结构。
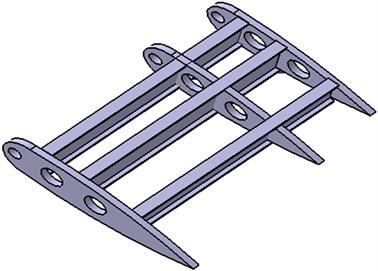
Figure 8. Multi-beam ribbed wing structure
图8. 多梁加肋的机翼结构
6. 结束语
本文主要以机翼结构布局为背景,在某种特定的情况下,根据载荷分布来进行有限元分析,实现机翼的最优拓扑结构。根据拓扑优化分析,在满足最大刚度的条件下,得到机翼内部翼梁和翼肋雏形,为机翼概念设计提供理论依据。本文采用拓扑优化的主要目的是确定机翼翼梁的大致数目与位置,相当于给定了相应的传力路径,拓扑优化结果要求不是很高。后期将会对优化结果进行详细论证分析,将更多的机翼翼型参数作为优化设计变量,但这将大大增加计算量,因而需探索有效的措施来减少计算量,为现实中机翼结构概念设计提供一定的参考价值。
基金项目
辽宁省自然科学基金(20180550526)。
文章引用
赵红娟,林伟航,魏 闯,杜家毅. 典型机翼的拓扑优化方法研究
Research on Topology Optimization Method for Typical Wings[J]. 国际航空航天科学, 2019, 07(01): 1-10. https://doi.org/10.12677/JAST.2019.71001
参考文献
电 话:400-123-4567
传 真:+86-123-4567
手 机:13800000000
邮 箱:admin@eyoucms.com
地 址:广东省广州市天河区88号