浅谈拓扑优化在建筑结构领域中的应用（一）

在开始谈拓扑优化(Topology Optimization)之前，让我们先回顾一下2016年的诺贝尔奖：物理学奖颁给了戴维?索利斯，邓肯?霍尔丹以及迈克尔?科斯特利茨，以表彰他们在理论上发现了物质的拓扑相变和拓扑相。拓扑学是三位得奖者能做出这一成就的关键，它解释了为什么薄层物质的的电导率会以整数倍发生变化。

我第一次接触到拓扑学这个概念，还是在百度搜索莫比乌斯环时顺带看到的。第一时间就感觉这个词很酷很炫，点开百度百科详细一读之后发现，自己是懵逼的。

无论是标题的拓扑优化，还是前面提到的拓扑相变和拓扑相，都离不开“拓扑”两字。给人一种“每个字都认识，但是连起来就不知道说了啥”的感觉，但偏偏就是这样引起了很多人的兴趣。

那么，到底什么是拓扑学呢？

按百度百科的说法，拓扑学音译自Topology，直译为地质学，是一种描述区域特征的地理学分支。后来扩展为数学领域上的几何学问题，是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。简单的说，它就是研究形态相似的程度。

其中，拓扑关系是指满足拓扑几何学原理的各空间数据间的相互关系。即用结点、弧段和多边形所表示的实体之间的邻接、关联、包含和连通关系。

这句话什么意思呢？

举个简单的例子

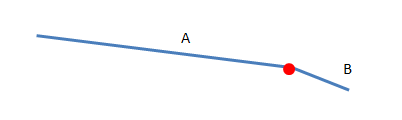
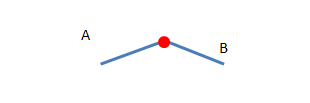
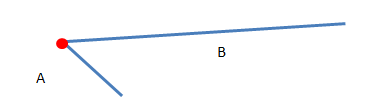
以上的A杆和B杆虽然长短不一，位置不一，但是它们都是通过一个小红点相连在一起的，我们可以说它们都具有同样的拓扑关系，也就是说它们都是拓扑等价的。

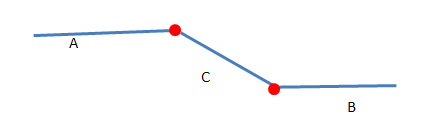
然而，在图5中，A与B拓扑关系发生了改变。

在拓扑学里面，三角形和正方形和圆形是等价的几何图形。你可以想象它们都是由一块橡皮泥揉成的，你可以将它任意地拉伸、压缩、弯曲，只要不撕破，也不使它粘连，这样变形后的图形跟原图形是拓扑等价的。因此，拓扑学也被成为橡皮几何学。

那拓扑学跟拓扑优化有什么关系？

所谓的拓扑优化，就是对于给定的材料，在它可能存在的所有拓扑关系里面，寻求一种能够满足优化目标的拓扑关系。也可以说，拓扑优化就是为了满足某种性能目标，在给定的荷载和边界条件下，寻求设计域中材料的最优空间分布的过程。

好吧，我说人话：拓扑优化其实是一个优雅地开洞的过程。

举个栗子：

七夕又到了，又到了牛郎去找织女的日子。以往在这一天牛郎要过银河的话，需要靠喜鹊们搭起像下面的这么一座桥（就把它脑补成桥吧….），需要起码一亿只的喜鹊才能搭起来，可是今年玉帝给牛郎出了个难题，这次只派出五千万只喜鹊给牛郎，让他来考虑怎么搭桥。虽然喜鹊不够，牛郎还是想将就着建一座桥，不然我就没法过去找对河的织女了。但是作为一个放牛娃，牛郎这辈子做过最聪明的事情就是把织女的衣服给藏了起来（还是在老牛的指导下），要利用现在的喜鹊来搭桥，真是难为他了。速成桥梁工程？学习是不可能学习的，这辈子不可能学习的。

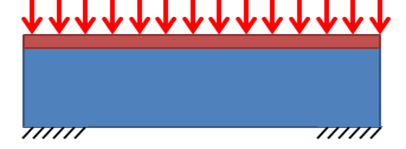
于是牛郎找到了我，问我能不能在这座桥原来样子的基础上把去掉一半的喜鹊，还能让他让我顺利地过河去找织女呢？作为从没接触过桥梁的一个结构小硕，我沉吟了一下，觉得是可以做到的：拿出《开洞是门技术活》(《A 99 line topology optimization code written in MATLAB》[1])这本书，根据上面的指示，按照某种算法，一边摆弄算盘，一边着手把不需要的喜鹊给去掉（挖洞），历经九九八十一个“迭代步”，终于赶在七夕前，利用仅有的喜鹊，把鹊桥给设计好了。

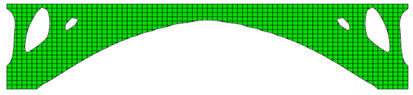
最后优化设计出来所得到的鹊桥跟赵州桥貌似有点像啊……啊，不管了，总之我就只用了原来一半数量的喜鹊就能把鹊桥搭好，让牛郎顺利过河去找织女了。

可以看到，赵州桥这座中国最知名的桥梁，其实就蕴含着最朴素的拓扑优化的理念。这是古人在考虑桥体承受一定载荷的作用下,设计出最简洁、结构整体刚性最好的桥体结构。

事实上，人类所处的世界，就是一个被优化过的世界，而大自然就是它的优化工程师。大自然中的花瓣形状就是通过拓扑优化可得到的最优解：

通过上面的小例子，我想大家应该能基本明白拓扑优化到底是什么回事了吧~事实上它跟拓扑学基本没有任何关系了，只是相较于传统的优化方案（形状优化和尺寸优化），只有拓扑优化能改变材料的拓扑性质。

嗯……所以不懂拓扑学是什么回事对你理解和学习拓扑优化也是没有太大影响的！（严肃脸.jpg）当然啦，拓扑学本身也是一门很有趣的学科，大家另外有时间的话也可以去钻研一下~

根据研究对象的不同，拓扑优化又可分为以下两种不同的方法：离散体结构（Discrete structure）拓扑优化方法和连续体结构（Continuum structure）拓扑优化方法。不管是哪个方法，都要依赖于有限元方法。简单来讲，连续体拓扑优化是把优化空间的材料离散成有限个单元（壳单元或者体单元），离散结构拓扑优化是在设计空间内建立一个由有限个梁单元组成的基结构，然后根据算法确定设计空间内单元的去留，保留下来的单元即构成最终的拓扑方案，从而实现拓扑优化。

目前，拓扑优化多应用于精密机械、航空航天等行业。然而，作为当下结构优化领域的热点和难点，拓扑优化设计在建筑结构设计领域也同样有着十分广阔的应用前景。对于不同的具体工程，在不同的约束条件之下，可利用拓扑优化技术来对建筑物的不同形态进行探索。反过来讲，也可以是从建筑学的角度出发，通过结构分析，结合结构优化的思想来对寻求建筑物的最佳形态。由此看来，在建筑结构设计领域，拓扑优化能够在概念设计阶段发挥重要的作用，同时能够促进建筑师和结构工程师的协同工作，若能利用好这一技术，将能得到兼具建筑美学又符合结构性能的创新性的建筑形态。

这篇文章算是一个系列的开始，接下来将会陆续介绍拓扑优化在建筑结构中的应用以及相关的原理及算法。

参考文献：

[1]. Sigmund O (2001) A 99 line topology optimization code written in Matlab. Structural and Multidisciplinary Optimization