随着微分学的不断完善,与之相逆的积分学也开始发展起来.而定积分最初的出现,是为了解决实际问题中计算一种和式极限的问题.与微分中值定理相对应,积分学中也有一套较为完善的积分中值定理理论,而且积分中值定理在积分学中,也占据了重要的地位.

在一元积分理论中,积分中值定理包括积分第一中值定理和积分第二中值定理.它们都是微积分学中的基本定理,在理论上有着一定的重要地位,特别是在一些逻辑推理论证方面有较多的应用.
设f(x)是定义在区间[a,b]上的函数,在(a,b)中任意插入n-1个分点
a=x?<x?<…<x <x
=b
来划分区间[a,b],这一分法记作T.在每个小区间[x ,x
]中任取一点ξ,作和式σ=
,其中
,记λ(T)为
,(i=1,2,…,n)中的最大值,即λ(T)=
,当λ(T)→0时,如果和式极限存在,且此极限值不依赖于ξ的选择,也不依赖于对[a,b]分法T,称此极限为f(x)在上的定积分.记为
f(x)dx.
若函数f(x)在闭区间[a,b]上连续,则在[a,b]上至少存在一点ξ,使得
f(x)dx=f(ξ)(b-a).
这里的ξ是在[a,b]上取值,实际上,也可以在开区间(a,b)上取值,即ξ∈(a,b)时,定理同样成立.
证明略去
若函数f(x)与g(x)在闭区间[a,b]上连续,函数g(x)在[a,b]上可积且不变号,则[a,b]在上至少存在一点ξ,使得
f(x)g(x)dx=f(ξ)
g(x)dx.
若将“g(x)在[a,b]上可积且不变号”改为“g(x)在[a,b]上连续且不变号”,这里的 可在(a,b)上取值,定理同样成立

各种形式的积分第二中值定理叙述如下:
重积分有许多重要的性质和定理,本节讨论二重积分中值定理并加以相应推广,使其应用更加广泛.

若f(x),g(x)在[a,b]上连续且g(x) ,则存在ξ∈[a,b],使
由引理1知,存在 (a,b),使得
再运用引理1得,存在 ,使得
故有
设f(x,y),g(x,y)在平面区域D上连续且g(x,y) 0,其中D=[a,b]×[c,d],a,b,c,d为常数且在同一象限.则存在点
,使
(1)根据已知条件,函数g(x,y)必有界,设lgl L,函数f连续必可积,从而
=0.
其中T是将D分割成小区域 T→0表示分割越来越细,
是f(x,y)在
上的振幅.
记
,又f(x,y)g(x,y)可积,故对于分割T,I可表示成如下两部分之和:
(2)对于 ,由于
因此 ,从而当T
0时,
也必有根,并且
令
,
为连续函数,那么
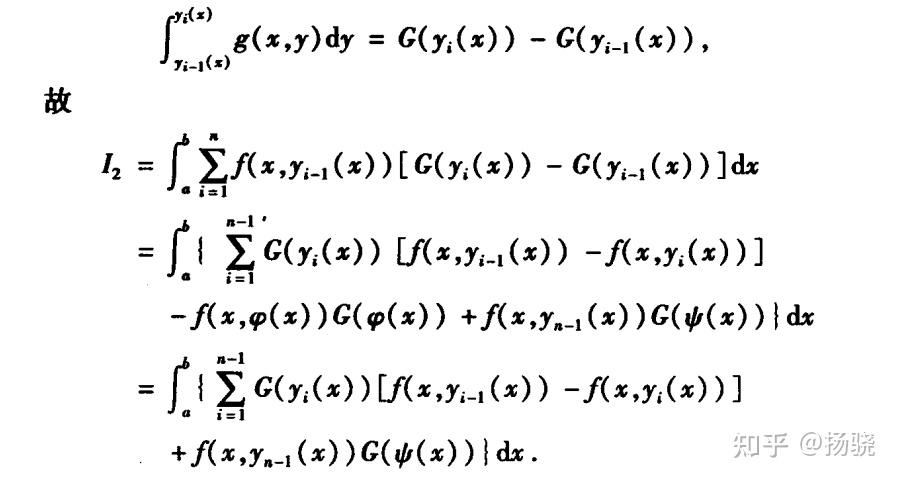
(3)
使
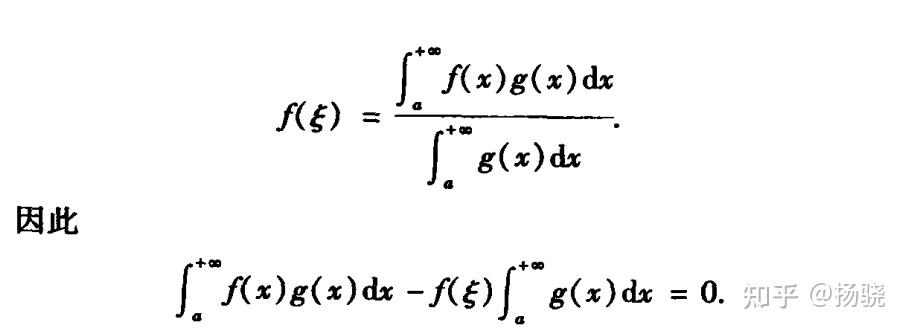
定理7 (关于无限区间上广义函数的广义积分第一中值定理)设函数f(x)在[a,+∞)上有界连续,函数g(x)在[a,+∞)上非负,并且 g(x)dx<+∞,则对任意ε>0,必存在一有限点
[a,+∞),满足
设 ,那么由
的非负性可知
(1)当
时,显然
(2)
时,由于g(x)非负,容易得到
,不妨设m<M(m=M时结论显然成立)。
如果 ,而
,存在
满足
那么
从而
如果
同理可证明出来
时,在[a,+
)上可取到
满足
则在
之间,必然存在
满足
因此

本定理的证法可采用类似定理7中的方法给出证明.
由于f(x,y)在C上连续,故由介值定理,在曲线C上至少存在一点,使
所以结论成立.
同理可证下面几个定理
其中A是曲面S的面积.
其中A'是S的投影D的面积.
与微分中值定理类似,积分中值定理也可以在复函数中推广,只是积分中值定理在复函数中的推广要比微分中值定理在复函数中的推广复杂一些.

引理2 设函数f(z)在单连通区域D内连续,且对D内的任意一条逐段光滑的简单曲线(以下简称围线)C,有
f(z)=0,则函数
(
为D内一定点)在D内解析,且
引理3 设函数f(x)在区域D内解析,则f(x)在D内具有各阶导数,且它们也在D内解析.
其中
定理 14 设函数
在单连通区域D内连续,且对D内任一围线C有:
,a为D内任意一点,则对点a的某邻域G
D及任意点
存在满足条件
,使
有
,g(z)=1时,
以上两个定理证明略去。
积分中值定理是定积分的重要性质,它建立了定积分与被积函数之间的关系,从而可以通过被积函数的性质来研究积分的性质,有较高的理论价值和广泛的应用.本章主要介绍了积分中值定理的简要概述,探讨了积分中值定理从三方面的推广:在黎曼积分上的推广;在曲面、曲线积分上的推广以及在复函数中的推广.
电 话:400-123-4567
传 真:+86-123-4567
手 机:13800000000
邮 箱:admin@eyoucms.com
地 址:广东省广州市天河区88号